峰 不二子じゃなくてゴメンナサイ

いやぁ～～～　前回はSLの話どころか回転の話すら出てこなかったですねあららら

かなり、やっちまたなぁ！！　って感じですけど

今回は、いよいよ回転に関するお話ですので、ちょっとはマシかもです・・・・・・







５．回転を表す四元数


さて、いきなりですが

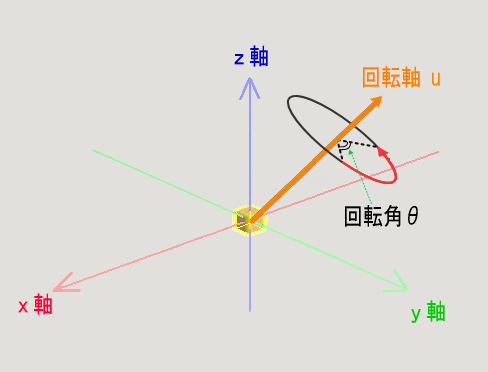
３次元の回転は、どのような回転であっても１本の回転軸と回転角によって決定します。


こんな感じです↓

　　　






で、この回転を四元数を使って表すんですけど、

原点を通る単位ベクトル u = ( α , β , γ )　を回転軸として、角度 θ の回転は、



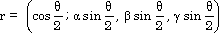　　　 　・・・・・・(5.1)



という四元数が対応します。（特に名前がないので、勝手に回転四元数とでも命名しておきましょう＾＾）

ここで、u は単位ベクトルですので、α ² + β ² + γ ² = 1 で、
回転の向きはベクトル u の方向に右ねじが進むときの回転方向です。（いわゆる右手系ってやつですね）




さて、同じ回転軸における回転角 θ の逆回転を表す四元数 r ' を考えると、


　　


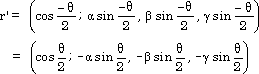
となり、r ' は r の共役四元数と一致します。　　　　　　　←定義(4.0)より

さらに、絶対値の平方を計算すると、　 　　　　　　　　　　←定義(4.1)より


　　　　　


となるので、r ' および r の絶対値は 1 と等しくなり、
r ' は r の逆数とも一致します。　　　　←定義(4.3)より

まとめておくと、

　　r ' = r = r^-1

ですね。すなわち、共役四元数や逆数が逆向きの回転を表すというわけですね


SLでの利用法として、オブジェクトの回転を相殺するためには、回転四元数の共役四元数をかけるか、
回転四元数で割ればいいことになります。



また、複数の回転を合成する場合は、それらの回転四元数をかければOKです。
この際、３次元の回転ですし、四元数は乗法に関して非可換なので、かける順序に気をつけなければです＾＾ｖ

例えば、２つの回転四元数 r 、s の積 r s は、まず r の回転をした後に s の回転をするといった具合に
かけていく順に回転していきます。




【LSLでは】

　　この回転四元数は、llAxisAngle2Rot (vector axis , float angle) という関数を用いれば、
　　一発で計算してくれます。

　　axis には、回転軸をベクトル型で記入します。この関数は、単位ベクトルでなくてもちゃんと換算するみたいです。
　　angle には、回転角をラジアンで記入します。


　　逆に、回転四元数から回転軸のベクトルおよび回転角を計算するのは、それぞれ
　　llRot2Axis(rotation rot) , llRot2Angle (rotation rot)  を使えばOKです。







６．ベクトルを回転させる


さて、いよいよ四元数を使ってベクトルを回転させましょう

と、その前に・・・

３次元のベクトルと四元数を直接は計算できないので、ベクトルを四元数にいったん変形しておく必要があります。
と言っても、そんなに難しい話ではなくて、ベクトルの各成分を虚部にそのまま対応させた四元数を考える
だけなんですけどね。（虚部のことをベクトル部とも言ったりします）

実部はどんな数でも構わないはずですけど、計算が楽なので０にしちゃいましょう。


具体的には、ベクトル v = ( x , y , z ) に対応する四元数は、 V = ( 0 ; x , y , z )  となり、これを
　　
　　V= ( 0 ; v )

 と表したりもします。





さて、どんどん話が進んでいきますけど、３次元のベクトルを四元数を用いて回転させてみましょう！！
下の図のように、ベクトル v を単位ベクトル u を回転軸として θ だけ回転させて、ベクトル v ' になったとします。




　　　　



２つのベクトル v と v ' は、V = ( 0 ; v ) 、 V ' = ( 0 ; v ' ) のように四元数に直してですね、
回転軸が u で回転角が θ なので、先ほどの回転四元数 r とその共役四元数 r  を使って、
次のような関係式が成り立ちます。


　　　　V ' = r  V r ・・・・・・(6.2) 　　おっと、文字が大きすぎたかな


とまぁ、このような感じで、元のベクトルを表す四元数に　回転四元数とその共役四元数を前後から挟み込むようにして　
かけ算すると、回転後のベクトルを表す四元数になるわけです。
なぜこうなるのかという話は非常にヤヤコシイので次回にでも　おいおい、やるつもりなのか＾＾；；


　　　　　



【LSLでは】

　　つい最近まで知らなかったんですけど、ベクトルに回転四元数を直接右からかけると、自動的に
　　上記のような四元数で挟み込むかけ算をして、その結果をベクトルで返してくれるみたいです。
　　例えば、回転前のベクトル v 、回転四元数 r に対して
　　　　　v * r
　　とするだけで、回転後のベクトルを一気に計算してくれるんですよ。
　　同様にわり算も定義されていて、
　　　　　v / r
    とすると、逆向きに回転させた後のベクトルを返すみたいです。


　　そんなこととは知らずに、今までずっと　上のような面倒くさい成分計算をしていました・・・・・ ガァーーーッ









７．回転の応用



上の話では、回転軸として原点を通るベクトルを考えましたけど、
一般には、原点を通らない軸に対しても回転は計算することができます。

といっても、そんなに難しい話ではなくて、

　　①回転軸が原点を通るように平行移動　
　　　　↓
　　②(6.2)の挟み込みのかけ算
　　　　↓
　　③回転軸が元に戻るように平行移動


といった感じで、基本的には(6.2)の原理を使います。


ただ、SLでは回転軸は原点を通るものに限定されますので、こういう技は使えないんですけどね・・・・＾＾；；
　（回転ドアを作るときには、パスカットして回転軸が端っこに来るように　しなきゃですよね。）　　










とまぁ、今回はこのへんで＾＾